햐 이거 알고리즘 공부 아직 얼마 안했을 때 봤던 문제인데..
너 무 어려웠다!! 당시에 이 문제의 해답을 보고도 이해가 안돼서 좌절했던 기억이 있다.
이걸 첨 본게 언제더라.. 1년은 된거같다. 아마?
지금의 나는 오토마타도 공부하고 DP도 공부해서 이런 문제쯤이야..! 풀 수 있지 않을까! (자신감없음)
전체 탐색 이해하기
DP의 시작은 전체 탐색이라고 했다.
그리고 그 과정에서 중복을 찾아 메모해야겠지.
일단 간단한 예시로 노가다를 해보자

아아.. 네모에다가 위, 아래에 문자열을 써놨는데 각각 string이랑 pattern이다.
매칭하고 남은 문자열을 써놓는 표기법이다.
처음에 s="string"과 p="st??**"의 맨 앞글자 s가 매칭되고 나서 "tring"과 "t??**"만 남은게 보일 것이다.
s가 p랑 매칭되는 경우의 수는 세 가지다
(맨 앞글자 기준으로)
1. s랑 p랑 같은 알파벳
2. s가 알파벳, p가 ?
3. s가 알파벳, p가 *
1번 2번의 경우는 정말 처리하기 쉽다.
그냥 매칭되는 글자를 s랑 p에서 빼버리면 된다. 아유 쉬워.
s랑 p랑 앞글자가 다른 알파벳이면 그냥 return False 때려버리면 되고.
문제는 .. *!
이 더러운 와일드카드가 문제를 야기한다.
그냥 간단하게 생각해봐도,
s = "ng"
p = "**"가 남았다.
*는 빈 문자열부터 모든 길이의 문자열과 매칭될 수 있으므로
p의 앞글자 *를 s랑 매칭하고 나면 나오는 결과가 세 가지다
s="ng" p="*"
s="g" p="*"
s="" p="*"
만약 s가 "string" p가 "**"라면?
s="string" p="*"
s="tring" p="*"
s="ring" p="*"
s="ing" p="*"
...
아 ㅋㅋ;;
감을 잡기 위해 노가다를 좀더 해보자
s = "string"
p = "*t**"의 경우다
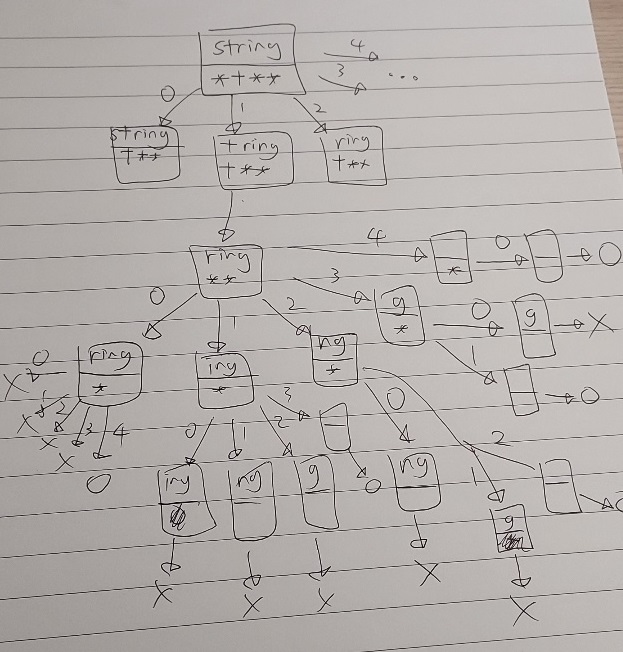
트리 간선에 있는 숫자는 몇 개의 글자를 매칭할지를 나타내는 거다.
맨 끝 X, O는 매칭이 성공했는지 실패했는지 여부를 나타낸다.
아직 유의미한 중복을 찾기는 어렵다.

s = "string"
g = "s*g"의 경우이다
여전히 중복은 보이지가 않는구먼
이번엔 초-극단적인 케이스로 가보자
s="aaaa"
p="***"

어..! 보인다 보여!!! 탐색트리에서 똑같은 노드가 보인다!!!
이제 직관으론 이해했으니 이걸 DP배열을 만들기 편하게 숫자로 나타낼수있어야겠지.

si,pi는 각각 문자열 s,p에 대한 index다. "여기부터 스캔해야돼요"를 나타내는 index. 그러니까 첨엔 둘다 0으로 시작한다.
자 이 si,pi를 이용해서 다시보자

si=2, pi=2인 부분이 중복되네? 그럼 이제 2차원 dp 배열을 하나 만들고 dp[2][2] = ~~ 이런식으로 메모를 해놓는거다. 저거 어차피 와일드카드로만 돼있어서 무조건 매칭되니까 dp[2][2] = True가 되겠구먼.
전체 탐색 구현
자 이제 직관적으로 이해는 스르르륵 해놨으니 전체 탐색을 구현하는 단계부터 시작한다.
class Solution:
def helper(self, s, p, si, pi):
if pi == len(p):
if si == len(s):
return True
else:
return False
if si == len(s):
if p[pi] == '*':
return self.helper(s, p, si, pi + 1)
else:
return False
if s[si] == p[pi] or p[pi] == '?':
return self.helper(s, p, si + 1, pi + 1)
if p[pi] == '*':
return self.helper(s,p,si,pi+1) or self.helper(s,p,si+1,pi)
return False
def isMatch(self, s: str, p: str) -> bool:
return self.helper(s, p, 0, 0)
종료조건이 생각보다 많이 복잡해졌다.
종료조건 정리하면서 막.. 깔끔하게 하려고 노력을 해봤는데 잘 안된다 ㅠ 일단 이정도로 만족하고..
굵을 글씨 친 부분을 잘 보아야 한다.
와일드카드는 0글자부터 모든 개수의 글자를 다 매칭할 수 있다고 했는데
이걸 0부터 반복문 돌려가면서 si를 건너 뛰어주는게 아니라 한 칸만 뛰어주고 재귀호출 했다.
그러면 해당 재귀호출 된 루틴 안에서 다시 si + 1을 호출 할거고 자연스럽게 0글자부터 모든 개수의 글자를 건너 뛰는게 구현이 될 것이다. 나중에 이걸 이용해 재귀를 없앤 구현도 가능하다 levenshtein edit distance랑 비슷하단 생각도 들었음 ㅋㅋ 그건 일단 나중에 보도록하고..!
Memoization 적용
진짜 정확히 위 코드에다가 memoization만 적용했다
class Solution:
def helper(self,dp, s, p, si, pi):
if dp[si][pi] != -1:
return dp[si][pi]
if pi == len(p):
if si == len(s):
dp[si][pi] = True
return True
else:
dp[si][pi] = False
return False
if si == len(s):
if p[pi] == '*':
dp[si][pi] = self.helper(dp, s, p, si, pi + 1)
return dp[si][pi]
else:
dp[si][pi] = False
return False
if s[si] == p[pi] or p[pi] == '?':
dp[si][pi] = self.helper(dp, s, p, si + 1, pi + 1)
return dp[si][pi]
if p[pi] == '*':
dp[si][pi] = self.helper(dp,s,p,si,pi+1) or self.helper(dp,s,p,si+1,pi)
return dp[si][pi]
dp[si][pi] = False
return False
def isMatch(self, s: str, p: str) -> bool:
dp = [[-1]*(len(p)+1) for _ in range(len(s)+1) ]
return self.helper(dp, s, p, 0, 0)

메모리 제외하고는 결과가 썩 나쁘지 않다. 코드도 좀만 깔끔하면 좋으련만ㅋㅋㅋ;; 여튼 내가 이걸 혼자힘으로 아무것도 안보고 풀어내다니 진짜 장족의 발전이다. 다른 사람은 recursion을 어떻게 구현했을까? 종료조건 어떻게 했을지 너무 궁금... (-> 나중에 다른사람들거 살펴봤는데 다른사람들도 if문을 떡칠해놨다. 이건 어쩔수없나보다)
재귀 없는 낭만적인 dp로 가볼까?
재귀 없는 dp를 설계하기 전에..
생각보다 머리아플 수 있다 정신 바짝 차리고 읽어보자.
재귀 없이 구현할 때는 dp[0][0]이 base case가 되는게 깔끔하다.
위에 재귀화 메모로 구현할 때는 (0,0)이 최종 정답이다.
하지만 재귀를 없애고 bottom-up dp를 하려면?
len(s),len(p)가 base case였으니 이걸 뒤집어줘야한다.
물론 그대로 두고 거꾸로 iteration 돌아도 되긴 하는데 찝찝하니까~
간단하다. 위에서는 f(si, pi)가 s[si:]와 p[pi:]의 매칭 결과였으니 이제는 s[:si+1] p[:pi+1]로 바꾸면 되지 않을까.
그러니까 전에는 '이 인덱스부터 문자열 끝부분까지의 매칭결과' 였다면 이제는 '문자열 시작부터 이 인덱스 전까지의 매칭결과'로 뒤집는 것이다. 그럼 f(0,0)이 base case가 될거고 f(len(s), len(p))가 정답이 되겠지. 그럼 dp배열을 만들어서 [0][0]부터 [len(s)][len(p)]까지 채워주면 된다.
근데 하나 생각해봐야될 게 있다. len(s) * len(p) 크기의 배열을.. 다 채워야 될까...?
극단적으로 s="abc" p="abc"인 경우를 생각해보자
| ∅ | a | b | c | |
| ∅ | T | |||
| a | T | |||
| b | T | |||
| c | T |
s[si]랑 p[pi]가 매치되면 si와 pi를 각각 1씩 증가시켰던걸 생각해보자. 위의 경우에는 위 4칸만 채우면 된다는 얘기다.
즉 dp배열 크기가 m * n이라면 꼭 m * n개의 칸을 다 채울 필요는 없는 것. 다 채우면 오히려 재귀보다 시간이 더 오래걸릴 것이다.
재귀로 구현할 때는
1. s[si]==p[pi]이거나 p[pi]가 '?'면 si랑 pi를 각각 하나씩 증가시켜 재귀호출했다
2. p[pi]가 '*'면 (1) si를 1 증가시키기도 하고 (2) pi를 1 증가시켜 두 가지의 재귀호출을 했다.
DP배열 관점에서 보면
(재귀로 구현할 때랑 지금이랑 인덱스가 뒤집어졌으니
재귀식 방법을 이 DP배열에 적용해보려면
여기서는 배열 오른쪽 아래 끝에서부터 거꾸로 보아야 한다.)
1. 제일 오른쪽 아래 칸이 목표 칸이다.
2. s[si]==p[pi]이거나 p[pi]가 '?'면 대각선(왼쪽 위)의 True/False 결과에 따라 값이 결정된다. 대각선으로 가본다.
3. p[pi]가 '*'면 위쪽칸이랑 왼쪽칸으로 둘다 가서 계산해본다. 둘중 하나라도 True면 True다.
if s[si] == p[pi] or p[pi] == '?':
return self.helper(s, p, si + 1, pi + 1) #대각선으로 가는거
if p[pi] == '*':
return self.helper(s,p,si,pi+1) or self.helper(s,p,si+1,pi) #왼쪽칸이랑 위쪽칸으로 가는거
이게 맞는지 한 번 hand simulation을 해보자~
오른쪽 아래에서부터 서치해보자.
예시는 s="abcdef" p="a?c*f"이다
| '' | a | ? | c | * | f | |
| '' | True (base) |
|||||
| a | True | |||||
| b | True | |||||
| c | True | True | ||||
| d | False | True | ||||
| e | False | True | ||||
| f | True |
s="aaaab"
p="*c"
매칭이 안되는 경우
| '' | * | c | |
| '' | |||
| a | |||
| a | |||
| a | |||
| a | |||
| b | False |
현재 글자가 매칭이 안되면 다른거 다 볼것도 없이 그냥 False다. ㅋㅋㅋ 빈공간 짱많네
s="aaaabaaa"
p="*b*"
| '' | * | b | * | |
| '' | True | True | False | True |
| a | False | True | False | True |
| a | False | True | False | True |
| a | False | True | False | True |
| a | False | True | False | True |
| b | True | True | ||
| a | False | True | ||
| a | False | True | ||
| a | False | True |
s = "aaaa"
p = "**"
| '' | * | * | |
| '' | True | True | True |
| a | False | True | True |
| a | False | True | True |
| a | False | True | True |
| a | False | True | True |
s="aaaa"
p="*b"
| '' | * | b | |
| '' | |||
| a | |||
| a | |||
| a | |||
| a | False |
s="abcd"
p="*zz"
| '' | * | z | z | |
| '' | ||||
| a | ||||
| b | ||||
| c | ||||
| d | F |
이정도면 핸드 시뮬레이션은 많이 돌린거같다.
이제 규칙을 찾아볼 시간이다.
| a혹은 '?' | ||
| D | U | |
| a | L | 이곳 |
'이곳'의 T/F는 어떻게 구할까?
위 표에서는 s[si]는 a고 p[pi]는 a혹은 '?'라고 했으니 s[si]와 p[pi]는 매칭된다.
그러니까 s[0 ~ si-1]이랑 p[0 ~ pi-1]만 매칭되면(D==True) s[0 ~ si]와 p[0 ~ pi]도 매칭된다고 할 수 있다.
따라서 D 칸의 True/False 여부가 '이곳'의 True/False를 결정한다.
L와 D의 T/F여부는 '이곳'에 영향이 없다.
물론 s[si]랑 p[pi]가 다른 알파벳이면 그냥 볼것도 없이 False다.
와일드카드는?
| * | ||
| b | D | U |
| a | L | 이곳 |
L이 True라면 와일드카드를 빈문자열에 매칭시킴으로써 '이곳'도 True가 된다.
U가 True라면 'b'를 와일드카드에 포함시킴으로써 '이곳'도 True가 된다.
그니까 L U 둘중 하나라도 True면 '이곳'도 True가 된다.
(U의 T/F 여부를 검사할 때 같은 논리로 D를 검사하게 될것이므로 D가 True면 당연히 '이곳'도 True가 될거다)
base case는 빈문자열-빈문자열인 경우고 base case까지 도달하면 매칭 완료다. 근데.. 우리는 낭만 있는 dp를 해야되지 않는가.. 이건 재귀를 이용해서 거꾸로 top-down으로 계산할 때나 이렇게 하는거고. bottom-up으로 하는 낭만을 이뤄보자.
이제 역방향말고 순방향으로 전파시키려면
| 좌상 | 위쪽 | |
| 왼쪽 | 현재 | 오른쪽 |
| 아래쪽 | 우하 |
패턴이 와일드카드가 아니고 글자가 매칭되는 경우는 좌상이 True일 때 현재가 True가 된다.
패턴이 와일드카드면 좌상, 왼쪽, 위쪽 중 하나라도 True일 때 현재는 True가 된다. 그리고 아래쪽도 전부 True가 된다. 그 다음엔 현재의 오른쪽과 아래쪽의 오른쪽, 아래아래쪽의 오른쪽, 아래아래아래쪽의 오른쪽을 다 구해봐야된다.
일단 비효율적인 dp를 해보자 (dp배열 다 채우기)
class Solution:
def isMatch(self, s: str, p: str) -> bool:
dp = [[False]*(len(p)+1) for _ in range(len(s)+1) ]
for si in range(len(s)+1):
for pi in range(len(p)+1):
if si == 0 and pi == 0: #base : dp[0][0]
dp[si][pi] = True
continue
if si == 0: #base : 맨 위쪽 행
if p[pi-1] == '*':
dp[0][pi] = dp[0][pi-1]
continue
if pi == 0: #base : 맨 왼쪽 열
dp[si][0] = False
continue
if s[si-1] == p[pi-1] or p[pi-1] == '?':
dp[si][pi] = dp[si-1][pi-1]
continue
if p[pi-1] == '*':
dp[si][pi] = dp[si-1][pi-1] or dp[si][pi-1] or dp[si-1][pi]
continue
return dp[len(s)][len(p)]

처참한 결과..ㅋㅋㅋㅋㅋㅋ
최적화를 해보자
일단 위에서는 base case를 따로 세팅하지 않고 반복문 안에서 if를 이용해서 채웠는데 이 경우 O(m * n)의 쓸데없는 if문을 실행하게 된다. 대부분은 base case가 아니니까 말이다. base case를 따로 빼내는것부터 최적화를 시작해보자.
class Solution:
def isMatch(self, s: str, p: str) -> bool:
dp = [[False]*(len(p)+1) for _ in range(len(s)+1) ]
#완전 베이스베이스베이스베이스 케이스
dp[0][0] = True
#맨 윗줄 채우기
#s=''와 p='*****'는 True다
#와일드카드가 시작부터 연속해서 나오는곳까지는 계속 True
#와일드카드 연속이 끊기면 그 뒤론 쭉 False
for i in range(1, len(p) + 1):
if p[i-1] == '*':
dp[0][i] = True
else:
break
for pi in range(1,len(p) + 1):
for si in range(1, len(s)+1):
if s[si-1] == p[pi-1] or p[pi-1] == '?':
dp[si][pi] = dp[si-1][pi-1]
continue
if p[pi-1] == '*':
dp[si][pi] = dp[si-1][pi-1] or dp[si-1][pi] or dp[si][pi-1]
continue
return dp[len(s)][len(p)]

base case만 따로 빼줬는데 성능이 크게 향상되었다. if문 네이놈.. 많은 자원을 먹고 있었구나!
근데 아직 찝찝하다. 배열의 대부분을 다 채운다는 점은 변하지 않았다. 아까도 살펴봤듯이 배열을 굳이 다 채울 필요가 없는데말이다. 불필요한 정보까지 다 구해서 계산하고 있다. (재귀의 경우에는 필요한 정보만 계산하기 때문에 지금보다 시간 성능이 좋게나왔다)
아 도저히 방법이 안떠오름..ㅋㅋ
---추가---
방금 초콜릿 먹다가 생각났는데.. 이거 grid 형태의 그래프라고 생각하고 스택이나 큐로 dfs나 bfs하면 되는거 아닐까?
아 근데 그러면 반복문으로 구현하는 맛이 안나는데.. 낭만이 없다ㅠ
참고로 공간적인 최적화는 간단하게 할 수 있다. 현재 열과 이전 열 (혹은 구현 방식에 따라 현재 행과 이전 행)만 사용되고 그 이전의 데이터들은 사용되지 않으므로 딱 두 줄만 있으면 계산하고 옮기고 계산하고 옮기고 하면서 space complexity를 O(min(len(s),len(p))로 만들 수 있다. 근데 시간적 성능은 완전 저하되겠지ㅋㅋ
내가 생각했던 최적화 방법을 구현했는데 효과가 크게 있진 않았다.
class Solution:
def isMatch(self, s: str, p: str) -> bool:
dp = [[False]*(len(p)+1) for _ in range(len(s)+1) ]
dp[0][0] = True
for i in range(1, len(p) + 1):
if p[i-1] == '*':
dp[0][i] = True
else:
break
si_min = 1
for pi in range(1,len(p) + 1):
tmp = 99999
for si in range(si_min, len(s) + 1):
if p[pi-1] == '*':
dp[si][pi] = dp[si][pi-1] or dp[si-1][pi]
if dp[si][pi]:
tmp = min(tmp, si)
if s[si-1] == p[pi-1] or p[pi-1] == '?':
tmp = min(tmp, si)
dp[si][pi] = dp[si-1][pi-1]
si_min = tmp
return dp[len(s)][len(p)]
매 iteration마다 탐색을 첫 인덱스부터 하는건 비효율적이니까 탐색을 시작할 최소 인덱스를 구해가면서 하는건데, 효과가 드라마틱하진 않았다. 66%.. 힝구..
다른 사람의 solution
class Solution:
def isMatch(self, s: str, p: str) -> bool:
s_idx = 0
p_idx = 0
star_idx = -1
s_temp_idx = -1
while s_idx < len(s):
if p_idx < len(p) and s[s_idx] == p[p_idx]:
s_idx += 1
p_idx += 1
elif p_idx < len(p) and p[p_idx] == '?':
s_idx += 1
p_idx += 1
elif p_idx < len(p) and p[p_idx] == '*':
star_idx = p_idx
s_temp_idx = s_idx
p_idx += 1
elif star_idx == -1:
return False
else:
p_idx = star_idx + 1
s_idx = s_temp_idx + 1
s_temp_idx = s_idx
return all(p[i] == '*' for i in range(p_idx, len(p)))
시간 90% 공간 98% 의 상위권을 달리는 엄청난 코드다.
굵은 글씨 친 부분이 뭔지 모르겠다. 핸드 시뮬레이션을 돌려봐야겠다
----
돌려봤는데도 모르겠다.
비슷한 방법을 쓴 다른 사람의 솔루션을 보자
def isWildcardMatch(self, s, p):
sn, pn = len(s), len(p)
si = pi = 0
save_si, save_pi = None, None
while si < sn:
if pi < pn and (p[pi] == '?' or p[pi] == s[si]):
si += 1
pi += 1
elif pi < pn and p[pi] == '*':
# Meet "*", save si and pi, searching for next character
save_si, save_pi = si + 1, pi
pi += 1
elif save_pi is not None:
# Dead end, restore si and pi, carry on.
si, pi = save_si, save_pi
else:
return False
# Check trailing "*"
return p[pi:].count("*") == pn - pi
좀더 가독성있는거같다.
이걸 보고 dp table이랑 같이 보니까 이해해버렸다... 와.. ㅋㅋ 이거 만든 사람 똑똑하네
dp[si][pi]가 True고 p[pi]가 와일드카드면 그 밑에는 다 True다.
| ... | * | |||
| ... | True | |||
| a | True | |||
| True | ||||
| True |
그러니까 와일드카드를 만나면 밑에칸 위치를 저장해놓고 최대한 오른쪽으로 탐색한뒤, 막히면 저장해놓은 위치로 돌아오는 일종의 dfs같다. dp 배열을 따로 만들지 않기 때문에 공간적인 효율이 엄청나고, 필요한 부분만 계산하기 때문에 시간적인 효율도 엄청나다. 대단하다 이 알고리즘
'코딩 테스트 및 알고리즘 > leetcode for google' 카테고리의 다른 글
| leetcode : next-permutation (0) | 2022.03.04 |
|---|---|
| leetcode : Permutations II (0) | 2022.03.03 |
| leetcode : Permutations [backtracking] 모든 순열 찾기 (0) | 2022.03.02 |
| leetcode : decode ways (0) | 2022.03.01 |
| leetcode : palindrome partitioning II (0) | 2022.02.25 |