Sum of Distances in Tree
https://leetcode.com/problems/sum-of-distances-in-tree/
Approach
모르겠다..;;
일단 트리 사이즈를 구해야될거같다는 직감이 들고
루트를 유동적으로 설정할 수 있다는 직감은 드는데
그 이상은 생각이 안난다.
Solution Study
솔루션을 공부하고 내 머릿속에서 재구성해서 썼다.
Intuition
각 노드에서 naive하게 dfs를 수행하면 O(N^2)으로 정답을 구할 수 있다.
하지만 O(N^2)으로는 TLE가 날것이다. (N이 최대 30000개다.)
우리는 이것을 O(N log N)이나 O(N) 수준으로 줄일 필요가 있다.
성능 최적화의 핵심은 연산의 중복을 줄이는 것이다.
Naive하게 계산할 때 어떤 중복이 있을지 고민해봐야 한다.
일단 중복을 줄이는게 목표니까 처음에 노드 한 개 쯤은 Naive하게 계산한다고 가정해보자.

노드 0의 sum of dist를 구했다.
0 → 1 : 1
0 → 2 : 1
0 → 1 → 3 : 2
⇒ 1 + 1 + 2 = 4
이제 이걸 알고 있는 상태에서
이 연산 결과를 최대한 활용해 다른 노드의 sum of dist를 빠르게 구해보자.
일단 쉽게 관찰할 수 있는 사실이 하나 있다.
0을 기준으로 sum of dist를 구할 때
간선 0 - 1 과 0 - 2는 한 번 혹은 여러 번 더해질 수 있다.
간선 0 - 1의 경우 1이 루트노드인 subtree에 또 다른 child들이 있어서 거기까지 가는 path를 더하면서 여러번 더해졌다. (아래 굵은 글씨 친 부분을 보자.)
0 → 1 : 1
0 → 2 : 1
0 → 1 → 3 : 2
⇒ 1 + 1 + 2 = 4
간선 0 - 1이 root의 sum of dist에 몇 번이나 더해질까?
잘 생각해보면 1을 루트노드로 하는 subtree의 사이즈다.
각 노드들에 한 번씩 방문하면서 간선 0 - 1을 지나가기 때문이다.
이 사실을 잘 기억하길 바란다.

이제 2를 기준으로 sum of dist를 구해보자.
2 → 0 : 1
2 → 0 → 1 : 2
2 → 0 → 1 → 3 : 3
1 + 2 + 3 = 6
0을 기준으로 구할 때와 어떤 중복이 있는지 발견하였는가?
잘 모르겠으면 간선별로 개수를 세어보자.
0을 기준으로 sum of dist를 구할 때
0 - 1 : 2개
0 - 2 : 1개
1 - 3 : 1개
2를 기준으로 sum of dist를 구할 때
0 - 1 : 2개
0 - 2 : 3개
1 - 3 : 1개
0 - 2의 개수가 달라졌다.
왜 달라진걸까?
방향이 달라졌기 때문이다.
간선 A - B에서 (A, B는 인접한 노드)
A의 sum of dist를 구할 때 간선 A - B가 몇 개나 더해지는지 구하려면
A → B 방향으로 가는 Path가 몇 개나 있는지 알아야 되고
B쪽에 있는 노드 개수만큼 B로 가는 Path를 셀 것이기 때문에
(B를 subtree로 봤을 때의 size of subtree B)가 (A - B 간선이 A의 sum of dist에 포함되는 개수)가 된다.
반대로 B의 sum of dist를 구한다면 B → A로 가는 Path가 몇 개나 있을까?
A쪽에 있는 노드의 개수만큼 있을 것이다. 즉 A를 subtree로 봤을 때의 size of subtree A가 된다.
아까 0 기준으로 구해볼 때 초록색으로 강조했던 부분을 다시 보면 쉽게 알 수 있을 것이다.
간선 0 - 1이 root의 sum of dist에 몇 번이나 더해질까?
잘 생각해보면 1을 루트노드로 하는 tree의 사이즈다.
각 노드들에 한 번씩 방문하면서 간선 0 - 1을 지나가기 때문이다.
이 사실을 잘 기억하길 바란다.
그림을 다시보자.
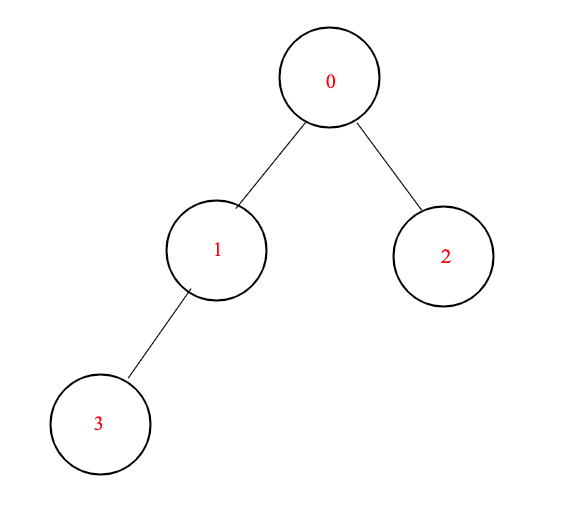
이제 sum of dist (parent)를 알면 sum of dist (child)를 쉽게 구할 수 있다.
parent와 child를 잇는 간선의 개수만 조절해주면 되기 때문이다.
sum of dist (child) = sum of dist (parent) - (parent에서 child로 가는 간선이 포함되는 횟수) + (child에서 parent로 가는 간선이 포함되는 횟수)
parent에서 child로 가는 간선이 포함되는 횟수 = size of (child)
child에서 parent로 가는 간선이 포함되는 횟수 = child에서 parent쪽으로 갈 때 도착점이 될 수 있는 노드 개수
= 전체 노드 개수 - child에 있는 노드 개수
= N - size of (child)
다시 정리하면
sum of dist (child) = sum of dist (parent) - size of (child) + N - size of (child)
= sum of dist ( parent ) - 2 * size of (child) + N
위에서 아래로 내려가면서 구해야 되니까
DFS 중에 preorder traversal을 하면 된다.
잠깐! 근데 이것은 우리가 루트 노드의 sum of dist를 알고 있다는 가정과 모든 subtree의 size를 알고 있다는 가정이 되어있다. 이것을 구하기 위해 제일 먼저 DFS( postorder traversal )를 해놔야 한다.
Algorithm
sizeOfTree[i] : 노드 i를 루트노드로 하는 subtree의 사이즈. 리스트다.
sumOfDist[i] : 노드 i의 sum of distance. 정답으로 리턴할 리스트다.
두 번의 DFS를 수행한다.
1. Postorder traversal
루트노드부터 탐색한다. 루트노드는 아무 노드나 될 수 있다.
left subtree의 size를 구하고 right subtree의 size를 구한다.
둘을 더한다음에 + 1(자기자신)한 값을 sizeOfTree[자기자신]에 저장한다.
sumOfDist[root]에 size of left subtree와 size of right subtree를 더한다. (subOfDist[root]에 left와 right subtree로 가는 간선이 포함되는 횟수) 혹은 sumOfDist[현재노드]에 sumOfDist[자식노드]와 sizeOfTree[자식노드]를 더해서 실시간으로 각 트리의 [루트노드에서 모든노드로 가는 path의 수]를 구해도 된다.
2. Preorder traversal
루트노드부터 탐색한다.
sumOfDist[현재노드] = sumOfDist[부모노드] - 2 * sizeOfTree[현재노드] + N
루트노드는 이미 계산되어 있으므로 계산을 생략한다.
Code Explanation
아.. 생각해보니 binary tree가 아니라 n-ary tree다. 위에 설명에서 left와 right subtree 라고 한 것들은 그냥 child라고 이해해주길.
class Solution(object):
def sumOfDistancesInTree(self, N, edges):
graph = collections.defaultdict(set)
for u, v in edges:
graph[u].add(v)
graph[v].add(u)
count = [1] * N
ans = [0] * N
def dfs(node = 0, parent = None):
for child in graph[node]:
if child != parent:
dfs(child, node)
count[node] += count[child]
ans[node] += ans[child] + count[child]
def dfs2(node = 0, parent = None):
for child in graph[node]:
if child != parent:
ans[child] = ans[node] - count[child] + N - count[child]
dfs2(child, node)
dfs()
dfs2()
return ansComplexity
노드 개수 N, 간선 개수 M
시간 복잡도는 O(N)이다. O(N)짜리 dfs를 두 번 했기 때문. (전체 노드에 한번씩 방문해서 linear time)
공간 복잡도는 O(M)이다. edges를 인접 리스트 형태의 그래프로 변환해서 저장하기 때문이다.
소감
이런게 라이브 코딩 인터뷰에 나오면 대체 어떻게 합격하나 구글은..
그곳엔 대체 어떤 인재들이 가는 것일까?
위 문제 leetcode discussion에도 이게 구글 인터뷰에서 나왔다면 면접관 어머니의 안부를 물어봐야 한다는 베댓이 있다 ㅋㅋㅋ..

이 문제를 풀고 자괴감을 느낀 분들 그럴필요 없다고 위로해주는 댓글도 있다.
자괴감이 드는 일요일 밤이다.
'코딩 테스트 및 알고리즘 > leetcode for google' 카테고리의 다른 글
| leetcode medium : 01 Matrix (Grind 75 Graph 문제 2) (0) | 2023.02.23 |
|---|---|
| leetcode easy : Flood Fill (Grind 75 Graph문제 1) (0) | 2023.02.22 |
| leetcode medium : Merge Intervals (Facebook 코딩 인터뷰 기출) (0) | 2023.02.19 |
| leetcode medium? : New 21 Game (0) | 2023.02.19 |
| leetcode hard : Best Time to Buy and Sell Stock IV (0) | 2023.02.16 |